时间复杂度和空间复杂度

时间复杂度(Big O notation)

O(1)：Constant Complexity 常数复杂度
O(log n)：Logarithmic Complexity 对数复杂度
O(n)：Linear Complexity 线性时间复杂度
O(n^2)：N square Complexity 平方
O(n^3)：N cubic Complexity 立方
O(2^n)：Exponential Complexity 指数
O(n!)：Factorial Complexity 阶乘

注意：
- 只看最高复杂度的运算
- 不考虑常数系数

计算时间复杂度

链接：如何计算时间复杂度和空间复杂度

最常用的方式就是直接看这个函数，或者是说这段代码根据n的不同情况它会运行多少次

int n=1000;
System.out.println("Hey - your input is:" + n);
//不管n等于多少，它的程序只执行一次，所以时间复杂度就是O(1)

int n=1000;
System.out.println("Hey - your input is:" + n);
System.out.println("Hmm..I'm doing more stuff with:" + n);
System.out.println("And more:" + n);
//同理，我们不关心前面的常数系数，虽然代码会执行3次，不管n是多少，它只执行3次，所以时间复杂度还是常数的，如果非要说的话O(3)也行，但其实就是O(1)因为它们都是常数级的
//在面试的时候千万不要说是O(2)O(3)O(4)这种，你就说是O(1)，或者常数时间复杂度

for(int i=1;i<=n;i++){
    System.out.println("Hey - I'm busy looking at:" + i);
}
//随着n的不同，代码运行的次数也会不一样，n=10000时，他会执行10000次，所以他的时间复杂度和n是成线性关系的所以记为O(n)

for(int i=1;i<=n;i++){
    for(int j=1;j<=n;j++){
        System.out.println("Hey - I'm busy looking at:" + i + "and" + j);
    }
}
//如果n=100，println会执行100x100次，他的时间复杂度就是O(n^2)
//如果for循环没有嵌套，是并列关系，那么代码就会执行2n次，不考虑常数系数，时间复杂度就是O(n)
//如果是3层嵌套，时间复杂度就是O(n^3)

for(int i = 1;i < n; i = i * 2){
    System.out.println("Hey - I'm busy looking at:" + i);
}
//O(log(n))

int fib(int n){
    if(n < 2) return n;
    return fib(n-1)+fib(n-2);
}
//O(k^n)

数据量越大，需要耗时越多，但是不同时间复杂度随数据量增长的速度是不一样的，有的算法对数据量增长比较敏感，数据量增长一点就会增加非常多的运算次数；有的算法对数据量增长不敏感，运行时间和数据规模呈线性关系。

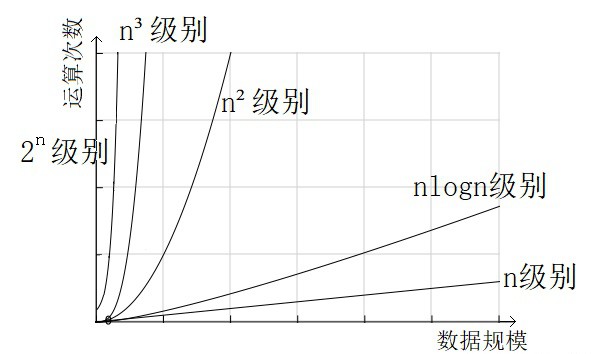
案例

计算1+2+3+...+n

方法一：从1到n的循环累加

y=0
for i=1 to n:
y+=i
#时间复杂度为O(n)

方法二：求和公式sum=n(n+1)/2
```
y=n*(n+1)/2
#时间复杂度为O(1)
```

递归

首先要了解递归总共执行了多少次语句。如果是循环就很好理解，循环了多少次就是执行了多少次。递归层层嵌套，很难辨别，其实很多时候我们要借助的就是把它的执行顺序画出一个树形结构图，我们称之为它的递归状态的行为树或者状态树。

案例

求fibonacci数列的第n项

Fib:0,1,1,2,3,5,8,13,21,...
F(n)=F(n-1)+F(n-2)

方法一：直接用递归

int fib(int n){
if(n<2) return n;
return fib(n-1)+fib(n-2);
}
//时间复杂度O(2^n)

主定理

链接：Master theorem
链接：主定理

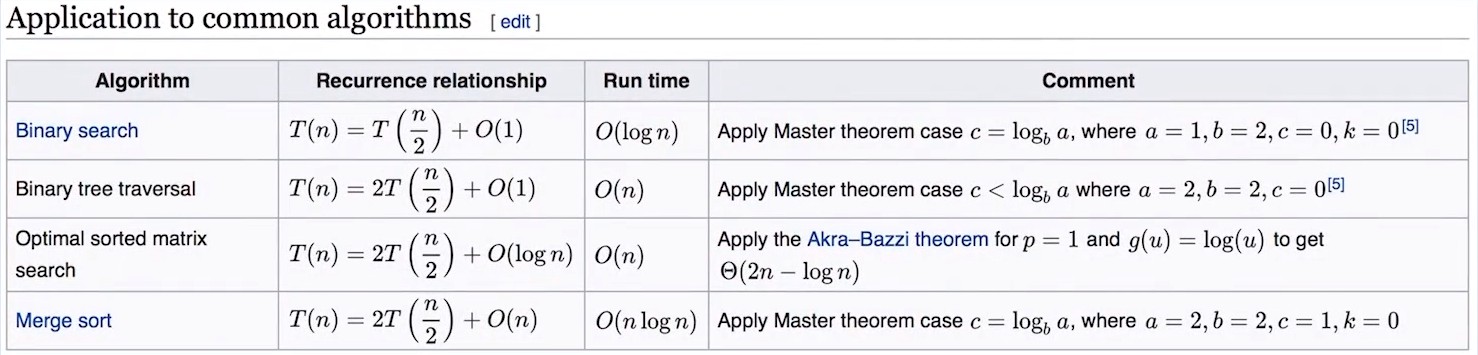
一般在各种递归情形下有4中情况是在面试和日常工作中用上的，

二分查找
一般发生在一个数列本身有序的时候，你要在有序的数列里找到你的目标数，所以它每次都一分为二，只查一边，这样下去，它的时间复杂度是O(log n)
二叉树遍历
时间复杂度为O(n)，他每次都要一分为二，每次一分为二之后都是相同的时间复杂度下去最后他的一个递推公式就变成了T(n)=2T(n/2)+O(1),最后用主定理可以推算出时间复杂度为O(n)
这里有一个简化的理考方式，二叉树遍历的话，我们每个节点都访问一次且仅访问一次，所以时间复杂度为O(n)
排好序的二位矩阵进行二分查找
时间复杂度为O(n)
这里记住如果是一维的数组进行二分查找就是logn，如果是有序的二位矩阵进行查找这时候被降了一维，就不是n平方的算法，而是O(n)的算法
归并排序
所有排序最优的算法就是nlogn，这个记住就好。所以归并排序也是nlogn的时间复杂度

思考题

二叉树的遍历-前序、中序、后序：时间复杂度是多少？

这个时间复杂度就是O(n)，这里的n代表二叉树里面的节点总数，可以直接说通过主定理这么得到的，更方便的一种分析方式，不管前序、中序、后序它遍历二叉树的时候每个节点会访问一次且仅访问一次，所以它的时间复杂度就是线性与二叉树的节点总数，也就是O(n)的时间复杂度

图的遍历：时间复杂度是多少？

同理，它每个节点会访问一次且仅访问一次，所以它的时间复杂度也是O(n)，这里的n代表图里面的节点总数

搜索算法：DFS、BFS时间复杂度是多少？

搜索算法DFS是深度优先，BFS是广度优先，这两个算法每个节点会访问一次且仅访问一次，所以它的时间复杂度也是O(n)，这里的n指的是搜索空间里的节点总数

二分查找

时间复杂度是O(log(n))

空间复杂度

1.数组长度
2.递归深度